나는 시각디자인학과고 2,3학년 동안 다른 전공수업을 찍먹해 보았다.
2학년 2학기
- 러시아어II - 러시아유라시아학과
3학년 1학기
- 컴퓨터그래픽스 - 소프트웨어융합학부
- C++프로그래밍 - 소프트웨어융합학부
- 웹클라이언트컴퓨팅 - 소프트웨어융합학부
3학년 2학기
- 영어학개론 - 영어영문학부
- 영어작문3 - 영어영문학부
- 선형대수 - 소프트웨어융합학부
결론부터 말하자면 다른 학과, 다른 단과대 수업을 듣는 것을 강력하게 추천한다. 가능하면 이른 시기부터 듣는 것을 추천한다. 조금이라도 흥미가 생기는 과가 있다면 고학년 수업이든 어려워 보이든 상관하지 말고 과감하게 수업을 들어보라고 하고 싶다. 특히 복수전공은 신청 기간이 제한되어 있어서 일찍 결정해야 한다.
힘든 점
일단 힘든 점은 서로 다른 주제들 사이를 스위치하는 것 자체도 적지 않은 에너지를 소모한다는 것이다. 3학년 2학기에 영어, 독일어, 선형대수, 디자인 프로젝트 2개를 동시에 했는데, 한 주제에 대한 몰입을 끊고 다른 걸로 옮겨가는 것이 어려웠다. 멀티태스킹의 신이 아니라면 어떤 분기의 메인 목표는 1-2개로 제한해야 집중력 누수를 줄일 수 있다. 나의 몸뚱아리는 하나고 머리도 하나다.
스위치를 할 때 이전에 공부하던 것의 남은 찌꺼기를 치워내고 예열을 하는 과정이 필요했는데 독일어를 공부하기 전에는 꼭 독일어 노래를 틀어야 했고 선형대수와 영어학개론을 공부하기 전에는 다른 책을 다 치우고 10분 이상 교재를 소리내서 읽어야 했다.
그리고 내가 레오나르도 다빈치도 아니고 평범한 대학생일 뿐인데 이것저것 다 공부하려면 밀도는 좀 떨어질 수밖에 없다. 근데 밀도는 좀 떨어져도 공부의 탄력은 올라가는 것 같다. 놀랍게도 3학년 2학기 거의 내내 수업과 공부가 재밌다는 생각을 하며 다녔다.
장점
서로 다른 단과대의 수업들이 하나의 시간표에 담기면 재미있는 일이 벌어진다. 머릿속에서 두 세계관이 하나로 합쳐지는 것이다. 하나의 단어를 서로 다른 맥락에서 공유하기도 하고(generic, morphology) 서로 부르는 단어는 다른데 개념이 일맥상통하기도 한다. 자세한 예시들은… 수업을 들은 이후로 시간이 지나서 까먹어서 못 적는다. 아쉽다.
선형대수 수업을 듣다가 갑자기 영어학개론 개념이 스쳐 지나가고, 영어학개론 수업을 듣다가 선형대수 개념이 스쳐 지나가서 강의 노트 한 구석에다 수업 내용과 상관도 없는 무언가를 끄적이는 재미가 있었다. 그리고 디자인 수업에서 컴퓨터그래픽스 개념을 끌고와서 작업할 때도 재미있었다.
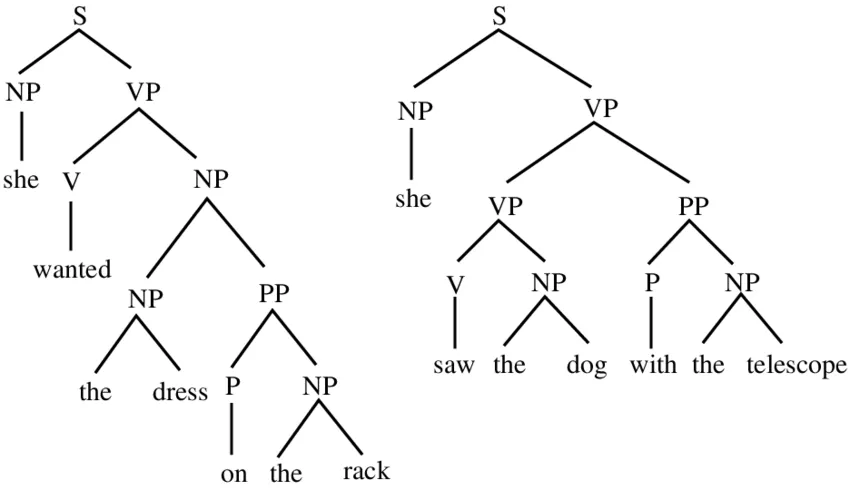
이 웹사이트에도 선형대수와 영어학개론의 크로스오버가 적잖은 영향을 미쳤다. 선형대수의 응용 예시에 대해 듣다가 네트워크 플로우 문제가 나왔는데 우연히도 그때 딱 이 웹사이트의 네트워크 그래프 부분을 개발하고 있을 때여서 되게 흥미롭게 들었다. 그리고 정말 공교롭게도 영어학개론 수업에서 트리구조가 나왔다. 영어 문장을 구 단위로, 단어 단위로, 그리고 마지막으로 morpheme 단위로 쪼개며 트리 그래프를 그리는 것이었다.
난 중첩된 폴더 구조의 노트 정리 방식에서 링크를 사용한 노트 정리 방식으로 옮겨간다는 큰 주제를 가지고 이 웹사이트를 만들고 있었는데, 마침 양 수업에서 등장한 네트워크 플로우 문제와 트리구조는 둘 사이의 차이점을 더 명확하게 인지할 수 있게 해 주어서 내 결정에 근거를 더해주었다.
내가 노션에서 만들어 사용하던 중첩된 폴더구조가 트리 그래프고, 옵시디언과 새로운 웹사이트에서 사용하는 링크를 이용한 구조가 네트워크 그래프였다. 둘은 노드에서 링크가 뻗어나간다는 점에서 겉보기에 비슷해 보이지만 이런 차이가 있다. (두 그래프에 대해 자세히 공부한 적은 없다. 그냥 두루뭉술한 내 이해가 이랬다 정도로만 봐주길…)
트리 구조의 예시
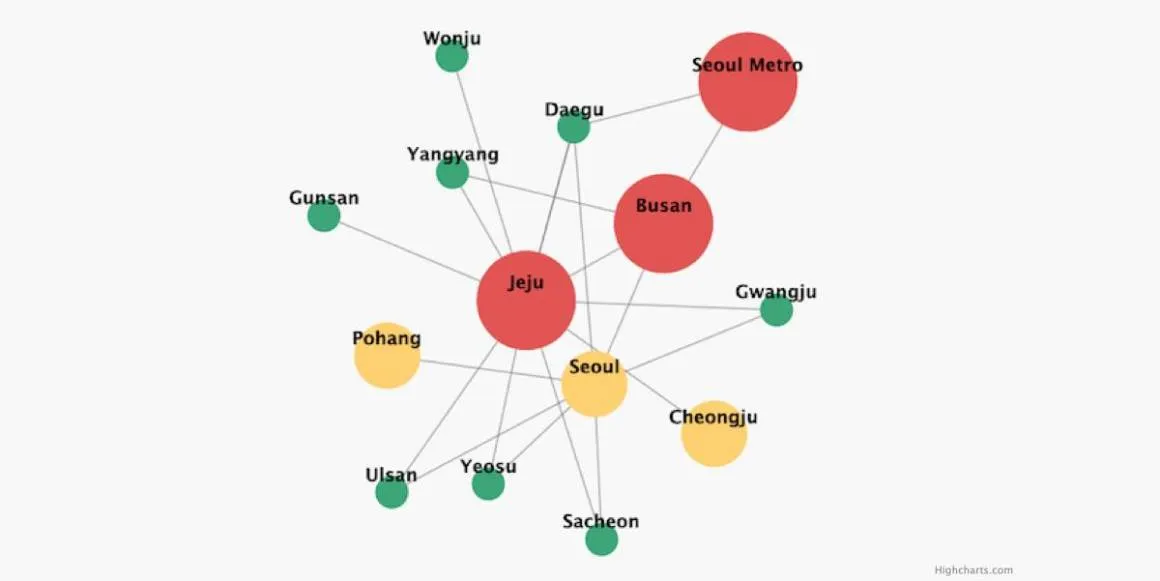
네트워크 구조의 예시
Trees vs Networks 차이점을 설명하는 블로그 글
| 트리 그래프 | 네트워크 그래프 | |
|---|---|---|
| node / edge 갯수 | n / n - 1 | n / 미정 |
| 두 node 사이의 path의 갯수 | 1 | 미정 |
| hierarchy와 root의 존재 | 있음 | 없음 |
| loop의 존재 | 없음 | 있음 |
모든 네트워크 그래프는 트리 그래프이지만 모든 트리 그래프가 네트워크 그래프인 것은 아니다. 네트워크 그래프만의 특징은 root가 없다는 것 즉 정해진 중앙이 없다는 것이다. 그리고 선형적이지 않다는 것이다. 네트워크 그래프는 한 node에서 나온 edge가 돌고 돌아 다시 자신이 나온 node를 가리킬 수 있다. 트리 그래프는 위계가 확실해서 자식이 부모를 가리키거나 다른 root를 가진 node와(이미 위에서 갈라져 나온 node와) 연결될 수 없다.
그래서 네트워크 그래프는 트리 그래프와 달리 이런 서로 다른 도메인들 사이를 연결하는 것이 가능해진다. 딱 내가 3학년 2학기에 하던 도메인을 넘나드는 생각들을 저장하기 좋은 형태인 것이다! 그래서 더 웹사이트에 애정을 갖고 작업할 수 있었다.